Напруженість електричного поля: Все, що вам потрібно знати
Задумайтеся на хвилину: ви тримаєте в руках електронний пристрій, і це поле, яке оточує його, безпосередньо впливає на вашу безпеку. Але що таке напруженість електричного поля? Як вона визначається і чому її важливо розуміти? Давайте розберемося.
Що таке напруженість електричного поля?
Напруженість електричного поля — це фізична величина, яка характеризує силу, з якою це поле діє на одиничний заряд, розташований у ньому. Простими словами, це «сила», з якою електричне поле «тягне» або «відштовхує» заряд.
Напруженість електричного поля визначається як відношення сили, з якою поле діє на заряд, до величини цього заряду. Це означає, що чим більша сила, тим сильніше поле, а чим більший заряд, тим більша буде сила взаємодії. Для людей, які тільки починають вивчати фізику, це може здатися складним, але насправді це дуже важливий аспект для розуміння, як працюють всі електричні пристрої навколо нас.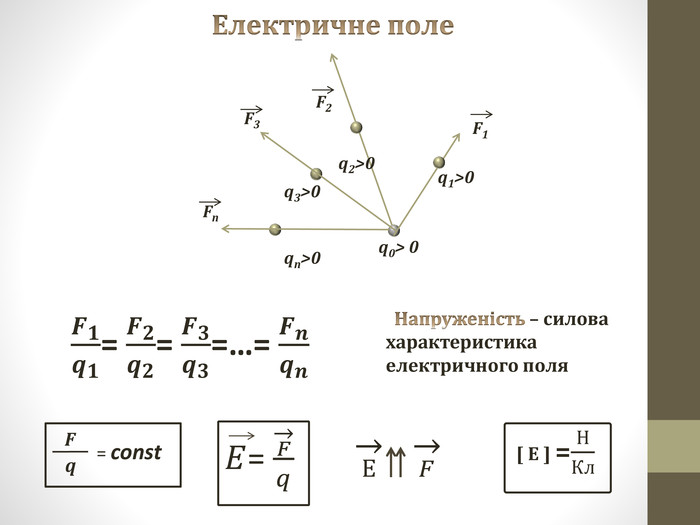
Як можна уявити собі напруженість електричного поля?
Уявіть, що ви тримаєте маленький заряд у руках і ставите його поблизу великого зарядженого об’єкта. Що станеться? Поле почне діяти на цей заряд, відштовхуючи чи притягуючи його, в залежності від знака заряду. Напруженість електричного поля буде визначати, наскільки сильно цей об’єкт впливає на заряджене тіло.
Приклад з побуту: розгляньте, як працюють електростатичні фільтри у кондиціонерах. Вони використовують електричне поле для «поглинання» пилу й алергенів. Як ви бачите, електричне поле не просто абстрактне поняття, а те, що має конкретне застосування в нашому повсякденному житті.
Як розрахувати напруженість електричного поля?
Розрахунок напруженості поля залежить від того, з якою конфігурацією зарядів ви працюєте. Один із основних підходів — це використання закону Кулона, який описує взаємодію двох точкових зарядів.
Закон Кулона стверджує, що сила взаємодії двох точкових зарядів пропорційна їх величинам і обернено пропорційна квадрату відстані між ними. Це означає, що чим більші заряди та менша відстань між ними, тим сильніша взаємодія. Для розрахунку напруженості поля, необхідно поділити силу на величину заряду. Це допомагає зрозуміти, як електричне поле «сприймає» різні об’єкти та надає числові значення для розрахунків у лабораторії чи в теоретичних задачах.
Важливість електричного поля в науці та техніці
Варто зазначити, що напруженість електричного поля не є лише академічною теорією. Це фундаментальне поняття, що лежить в основі багатьох технологій, зокрема в електроніці та обчислювальних системах. Наприклад, в дисплеях, що використовуються в мобільних телефонах чи телевізорах, електричне поле застосовується для управління яскравістю пікселів. В автомобільній промисловості — для роботи датчиків та систем контролю.
Теорема Гаусса: Як вона допомагає зрозуміти напруженість електричного поля?
Теорема Гаусса — це ще одне важливе правило, яке застосовується для обчислення електричного поля в складних ситуаціях. Вона стверджує, що електричний потік через будь-яку замкнуту поверхню пропорційний загальному зарядові, що знаходиться всередині цієї поверхні. Цей принцип застосовується для обчислення полів, коли у вас є симетричні заряди, такі як точкові заряди або заряджені кульки.
Наприклад, коли ви обчислюєте електричне поле навколо зарядженого провідника або вбудованого металевого об’єкта, теорема Гаусса дозволяє обчислити поле в загальному випадку, без необхідності враховувати кожен окремий заряд.
Як це працює в реальному житті?
Приклад з електричними приладами: коли ви тримаєте мобільний телефон чи комп’ютер, то можете не помітити, але навколо вас постійно є електричні поля, які керують функціями пристроїв. Чим більше напруженість цього поля, тим швидше й ефективніше працюють різні компоненти — від маленьких транзисторів до великих акумуляторів.
Вибухова тема в світі технологій — бездротові зарядні пристрої. Вони працюють завдяки змінам в електричних полях, що дозволяють заряджати ваші пристрої без кабелів. Все це стає можливим завдяки точним вимірюванням напруженості електричного поля.
Розуміння того, як працює електричне поле, допомагає не тільки в навчанні, але й у реальному світі. Це дозволяє не лише зрозуміти, як працюють різні пристрої, а й розвивати нові технології. Напруженість електричного поля є основою для бездротових технологій, електроніки і навіть для обчислень у фізиці.
Отже, кожен з нас може зацікавитися цим і використовувати знання для розуміння того, як працює навколишній світ. І хто знає — може, у вас з’явиться ідея для нового винаходу!







