Буває, що прості речі плутають більше, ніж складні. Так часто буває з геометрією — особливо коли мова йде про діагоналі ромба. У школі ми запам’ятовуємо формули, але рідко розуміємо, що вони означають насправді. А діагональ — це не просто лінія між вершинами. Це ключ до всіх властивостей ромба, його симетрії й навіть до площі.
Що таке діагональ ромба
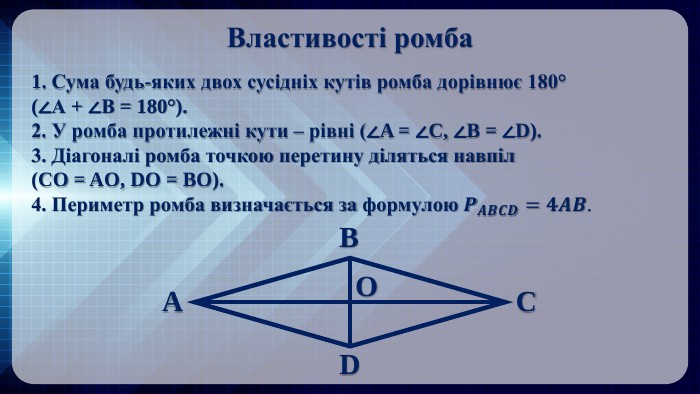
Якщо провести відрізок від однієї вершини ромба до протилежної — от і буде діагональ. Таких відрізків два. Вони перетинаються, ділять одна одну навпіл і завжди стоять під прямим кутом. Це означає, що діагоналі ромба перпендикулярні.
Уявіть собі ромб, схожий на витягнутий квадрат. Його діагоналі — це мовби осі, які розрізають фігуру на чотири однакові трикутники. І всі вони рівні, наче дзеркальні відображення одне одного.
Ще одна важлива річ — діагоналі ромба є бісектрисами його кутів. Тобто вони ділять кути навпіл. І саме тому ромб має таку гарну симетрію, коли обидві лінії діляться точно в центрі.
М’який висновок: якщо запам’ятати лише одне правило — діагоналі ромба завжди перетинаються під прямим кутом, — ви вже розумітимете більшість задач на цю тему.
Формули для діагоналей ромба
Усе в геометрії можна знайти через зв’язки. Так і тут: діагоналі ромба пов’язані з його стороною, кутами і площею. Основна формула, яку варто знати:
S = (d₁ × d₂) / 2,
де S — площа ромба, а d₁ і d₂ — його діагоналі.
Це означає, що якщо ви знаєте площу і одну діагональ, то легко знайдете другу:
d₂ = (2 × S) / d₁.
Наприклад, площа ромба 48 см², а одна діагональ дорівнює 12 см. Тоді інша діагональ — (2 × 48) / 12 = 8 см. Просто, правда?
Є ще одна корисна формула, якщо відома сторона ромба (a):
d₁² + d₂² = 4a².
Це правило випливає з теореми Піфагора, бо кожна діагональ утворює прямокутні трикутники.
Іноді задачі ставлять по-іншому: наприклад, відомий кут ромба α. Тоді можна використати формули:
d₁ = a × √(2 + 2cosα)
d₂ = a × √(2 – 2cosα)
Такі варіанти часто зручні для шкільних задач, де треба знайти всі елементи фігури.
М’який висновок: не запам’ятовуйте всі формули механічно. Виберіть ту, що підходить до умови задачі. Важливо розуміти, що діагоналі ромба пов’язані з усім його “внутрішнім життям” — стороною, кутами та площею.
Як зрозуміти діагоналі через приклади
Уявімо практичну ситуацію. Ви малюєте ромб для дизайну плитки. Одна діагональ дорівнює 40 см, інша — 30 см. Їхній добуток поділимо навпіл:
S = (40 × 30) / 2 = 600 см².
Тепер ви знаєте площу ромба без жодних складних вимірювань.
Або інший приклад: ромб має сторону 10 см, і кут між сторонами 60°.
d₁ = 10 × √(2 + 2 × 0.5) = 10 × √3 ≈ 17,3 см.
d₂ = 10 × √(2 – 2 × 0.5) = 10 × √1 = 10 см.
Ви бачите, що діагоналі не рівні — і це нормально. Рівні вони лише в квадраті.
М’який висновок: геометрія — не сухі формули, а спосіб бачити пропорції у світі. Якщо ви зможете пояснити цифрами будь-яку лінію, ви справді розумієте простір.
Навіщо знати про діагоналі ромба
Навіщо знати про діагоналі ромбаЗнання діагоналей допомагає не лише на уроках. Це база для креслення, будівництва, дизайну та навіть розрахунку площ у побуті.
Коли ви малюєте плитку, шиєте виріб або створюєте орнамент — усе зводиться до простих фігур. І саме діагоналі ромба дозволяють швидко знайти центр, рівні частини й симетрію.
У практичних задачах це означає: менше помилок, швидші розрахунки, гарний результат.
М’який висновок: геометрія не лише про теореми. Вона про точність і гармонію, які ми використовуємо щодня, навіть не помічаючи.
Діагоналі ромба — це дві лінії, що тримають усю фігуру в рівновазі. Вони ділять ромб на чотири однакові частини, показують його симетрію та дозволяють обчислити площу.
Запам’ятайте три прості речі:
Діагоналі ромба перпендикулярні.
Вони ділять одна одну навпіл.
Через них можна знайти площу або сторону ромба.
Математика стає легшою, коли ви бачите в ній логіку, а не лише цифри. Спробуйте пояснити діагоналі ромба дитині — і ви здивуєтесь, наскільки просто це звучить, якщо розумієш суть.
